Introduction
Lately, Artificial Intelligence has seen a significant growth in utility with the ability to solve increasingly complex problems. However, the required energy to operate these systems has also significantly increased [1]. To tackle this future problem, the neuromorphics field has taken inspiration from the brain and designed devices that both function as memory and processor [2], which is different from the conventional software architecture. These devices are constrained by their physical properties and this can result in difficulties when implementing conventional learning algorithms. That is why it’s crucial to explore alternative learning strategies that may utilize these physical properties [3]. The physical learning field utilizes the physical system to generate energy equations, where they can be separated by a free and clamped state, which describe what the system knows and what the system should know respectively. [4,5] There are many ways to separate these two states (duplicate network, physical separation), but in this project we focus on ‘Frequency propagation’ [6], where one signal contains both the free and clamped state that are separated by frequency, which allows them to be separated and compared via the Fourier Transform.
Project description
We have hypothesized a new device that contains two gates that are connected to the neuromorphic device’s channel by two separate electrolytes, as shown in Figure 1. If we assume a symmetric device at , the channel conductance should not change by applying opposite gating voltages with the same strength. To one of the gate we directly connect the voltage drop (within the project we’ll have design a circuit that takes the voltage drop and generates a pulse) and to the other gate we’ll let the voltage go through a low pass filter (LPF), thereby negating the clamped output effect. This means that the low pass filter only takes the information from the clamped input (free state), whereas the other gate takes both the information of the clamped input and output (clamped state). If we set the pulse strength the same and modulate the pulse length based on the voltage drop, the resistance should converge to the a state where the voltage drop of the free and clamped state is the same.
An intermediate goal is to make such a device and characterize its behavior to proof the hypothesis. If we conclude that learning with the hypothesized device is not possible, we’ll solve that problem with the electrical circuitry and continue with the conventional neuromorphic devices that are used in the group.
If we manage to realize learning with a single device by building a voltage divider that can perform allostery, we can extend the learning task to realize an XOR gate or a simplified classification with the iris dataset.
The proposed project has the following goals
· Realize the dual gate/dual electrolyte device
· Characterize the symmetry updating problem, where the same should not correspond to any change in the weight
· Design and model the required electrical circuitry necessary to perform frequency propagation
· Build a voltage divider to perform allostery
· Build a larger network to realize classification (XOR/iris data set)
Required skills
(Note: These skills are not required, but would be beneficial)
- Basic coding skills
- Electrical circuit design knowledge
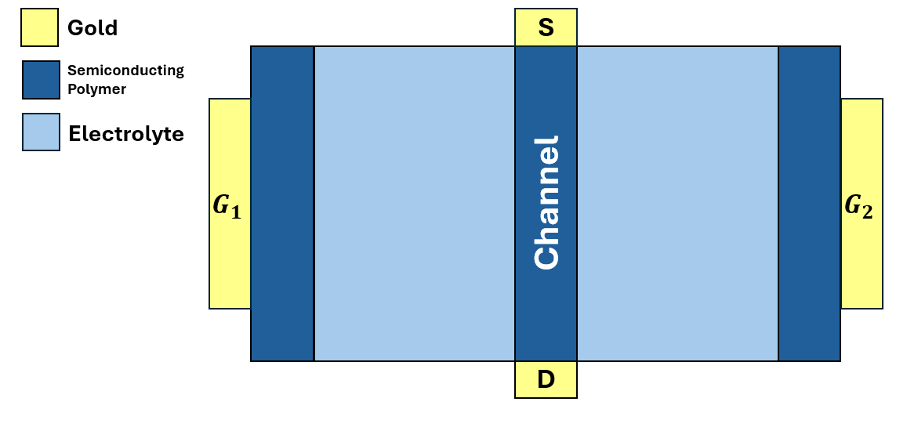
Figure 1. Visualization of the dual gate/dual electrolyte neuromorphic device
References
[1] Zolfagharinejad, eta al. Brain-inspired computing systems: a systematic literature review. The European Physical Journal B 97(2024). https://doi.org/10.1140/epjb/s10051-024-00703-6
[2] Van de Burgt, et al. A non-volatile organic electrochemical device as a low-voltage artificial synapse for neuromorphic computing. Nature Materials 16 (2017). https://doi.org/10.1038/NMAT4856
[3] Lv, et al. Towards Biologically Plausible Computing: A Comprehensive Comparison. arXiv. (2024). https://doi.org/10.48550/arXiv.2406.16062
[4] Dillavou, et al. Laboratory Demonstration of Decentralized, Physics-Driven Learning. arXiv. (2022). https://arxiv.org/abs/2108.00275
[5] Kendall, et al. Training End-to-End Analog Neural Networks with Equilibrium Propagation. arXiv (2020). https://arxiv.org/abs/2006.01981
[6] Anisetti, et al. Frequency propagation: Multi-mechanism learning in nonlinear physical networks. arXiv (2022). https://arxiv.org/abs/2208.08862

